Chapter 1: Elementary Signals

This chapter presents the elementary signals used in signal processing. These fundamental building blocks form the basis for analyzing more complex signals and systems.

Dirac Delta Function

Definition

The Dirac delta function $\delta (t)$ is a mathematical idealization representing an impulse of infinite height, zero width, and unit area.

$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\delta (t)dt=1\text{and}\delta (t)=0\text{ for }t\ne 0$$

While not a function in the classical sense, $\delta (t)$ can be understood as the limit of a sequence of functions. For example, using Gaussians:

$$\delta (t)=\underset{\sigma \to 0}{lim}\frac{1}{\sigma \sqrt{2\pi }}{e}^{-t^2/(2{\sigma }^2)}$$

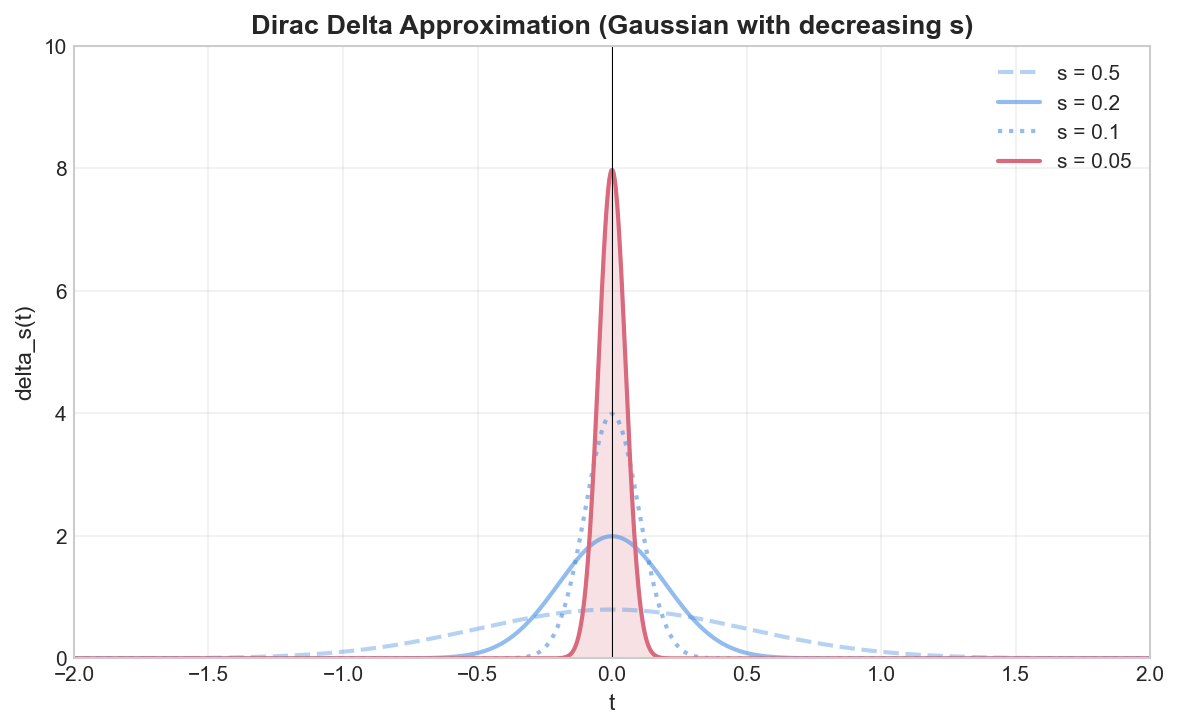
Properties

Sifting Property: For any function $f(t)$ continuous at $t_0$:

$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(t)\delta (t-t_0)dt=f(t_0)$$

Scaling Property:

$$\delta (at)=\frac{1}{|a|}\delta (t),a\ne 0$$

Derivative Property:

$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(t){\delta }^{\prime }(t)dt=-f^{\prime }(0)$$

---

Unit Step Function

Definition

The unit step function (Heaviside function) is defined as:

$$u(t)=\{\begin{array}{ll}1& \text{if }t\ge 0\\ 0& \text{if }t<0\end{array}$$

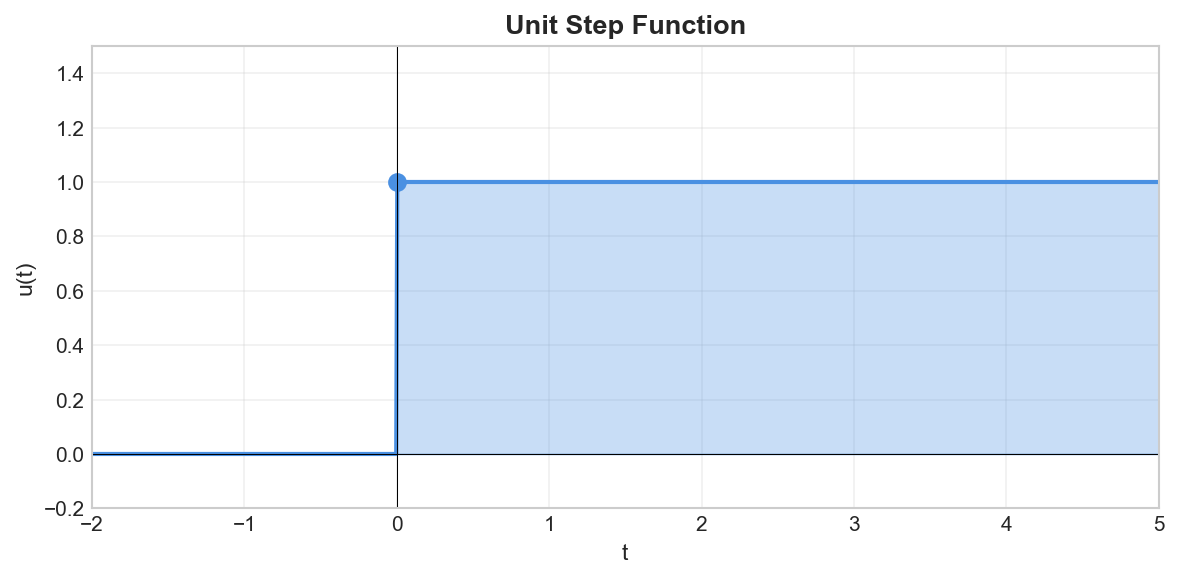
Properties

Relationship with Dirac Delta:

$$\frac{du(t)}{dt}=\delta (t)$$$$u(t)={\int }_{-\mathrm{\infty }}^t\delta (\tau )d\tau$$

Windowing: The unit step can be used to "turn on" a signal at $t=0$:

$$x(t)u(t)=\{\begin{array}{ll}x(t)& t\ge 0\\ 0& t<0\end{array}$$

Shifted Step: A step delayed by $t_0$:

$$u(t-t_0)=\{\begin{array}{ll}1& t\ge t_0\\ 0& t<t_0\end{array}$$

---

Unit Ramp Function

Definition

The unit ramp function is defined as:

$$r(t)=t\cdot u(t)=\{\begin{array}{ll}t& \text{if }t\ge 0\\ 0& \text{if }t<0\end{array}$$

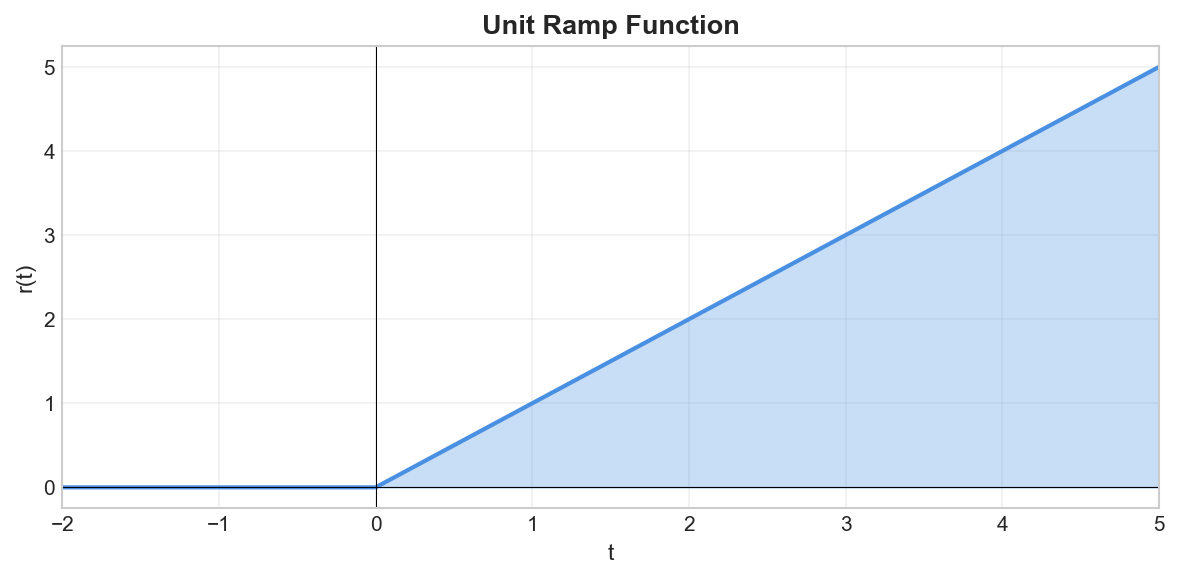
Properties

Relationship with Unit Step:

$$r(t)={\int }_{-\mathrm{\infty }}^{t}u(\tau )d\tau$$$$\frac{dr(t)}{dt}=u(t)$$

Relationship with Dirac Delta:

$$\frac{d^{2}r(t)}{d{t}^2}=\delta (t)$$

---

Complex Exponential

Definition

The complex exponential is defined as:

$$x(t)=A{e}^{st}=A{e}^{(\sigma +j{\omega }_0)t}$$

where:

• $s=\sigma +j{\omega }_0$ is the complex frequency
• $A$ is the amplitude
• $\sigma$ is the damping factor (attenuation)
• ${\omega }_0$ is the angular frequency (rad/s)

Using Euler's formula $e^{j\theta }=\cos (\theta )+j\sin (\theta )$:

$$x(t)=A{e}^{\sigma t}[\cos ({\omega }_{0}t)+j\sin ({\omega }_{0}t)]$$

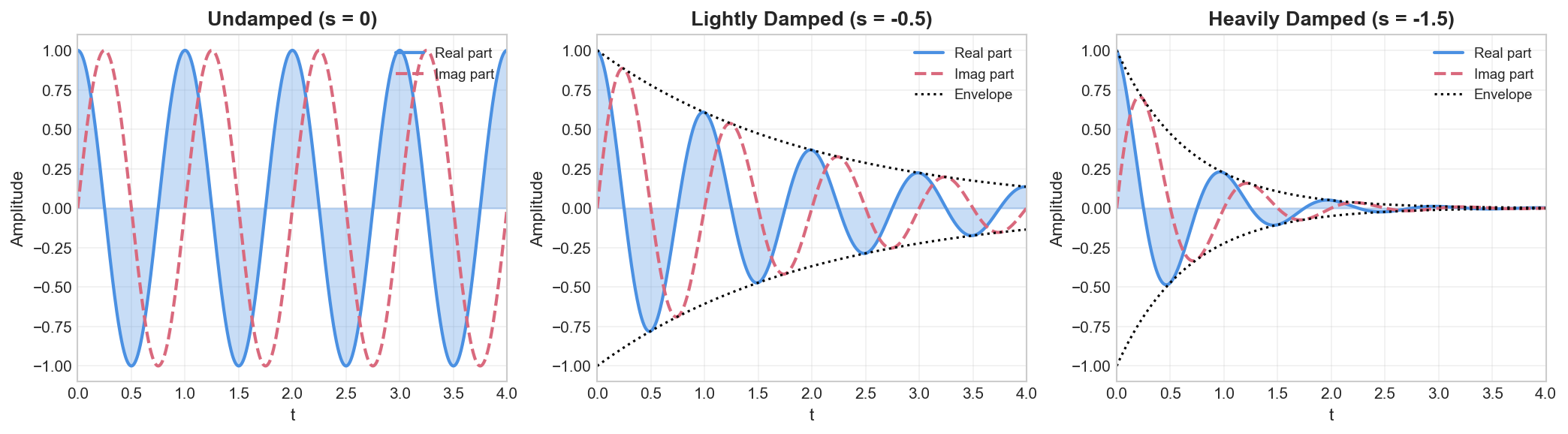
Properties

Euler's Formula:

$$e^{j\theta }=\cos (\theta )+j\sin (\theta )$$

Behavior based on $\sigma$:

• $\sigma =0$: undamped oscillation (constant amplitude)
• $\sigma <0$: damped oscillation (decaying amplitude)
• $\sigma >0$: growing oscillation (unstable)

Eigenfunction Property: Complex exponentials are eigenfunctions of LTI systems:

$$\mathcal{T}\{e^{st}\}=H(s)e^{st}$$

Periodicity: When $\sigma =0$, the signal is periodic with period $T_0=2\pi /{\omega }_0$.

---

Sinusoidal Signal

Definition

A sinusoidal signal is defined as:

$$x(t)=A\cos ({\omega }_{0}t+\varphi )$$

where:

• $A$: amplitude (peak value)
• ${\omega }_0=2\pi f_0$: angular frequency (rad/s)
• $f_0$: frequency (Hz)
• $T_0=1/f_0$: period (s)
• $\varphi$: initial phase (rad)

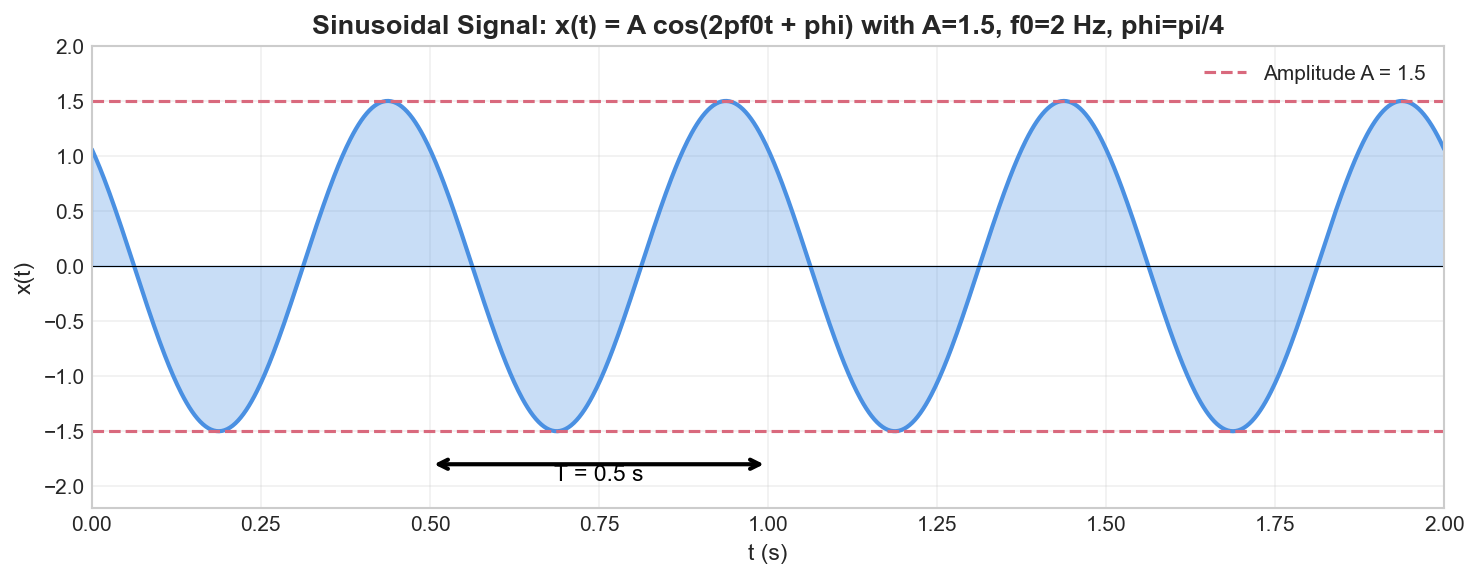
Properties

Periodicity:

$$x(t+T_0)=x(t)\text{where }{T}_0=\frac{2\pi }{{\omega }_0}=\frac{1}{f_0}$$

Relation to Complex Exponentials:

$$\cos ({\omega }_{0}t)=\frac{1}{2}(e^{j{\omega }_{0}t}+e^{-j{\omega }_{0}t})$$$$\sin ({\omega }_{0}t)=\frac{1}{2j}(e^{j{\omega }_{0}t}-e^{-j{\omega }_{0}t})$$

Power: A sinusoid is a power signal with average power:

$$P=\frac{A^2}{2}$$

Phase Shift: A time delay $t_0$ corresponds to a phase shift:

$$A\cos ({\omega }_0(t-t_0))=A\cos ({\omega }_{0}t-{\omega }_0{t}_0)$$

---

Rectangular Pulse

Definition

The rectangular pulse (gate function) of width $T$ centered at the origin is:

$$\text{rect}\left(\frac{t}{T}\right)=\{\begin{array}{ll}1& \text{if }|t|\le \frac{T}{2}\\ 0& \text{otherwise}\end{array}$$

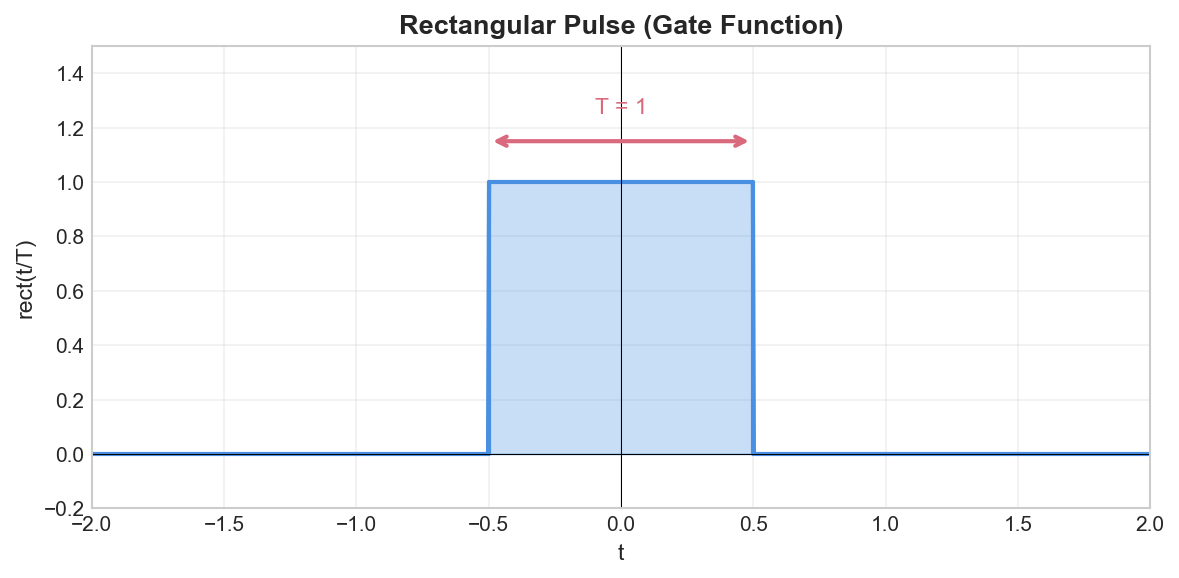
Properties

Relation to Unit Steps:

$$\text{rect}\left(\frac{t}{T}\right)=u(t+\frac{T}{2})-u(t-\frac{T}{2})$$

Area:

$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\text{rect}\left(\frac{t}{T}\right)dt=T$$

Energy:

$$E={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|\text{rect}\left(\frac{t}{T}\right)\right|}^{2}dt=T$$

Fourier Transform: The Fourier transform of a rectangular pulse is a sinc function:

$$\mathcal{F}\left\{\text{rect}\left(\frac{t}{T}\right)\right\}=T\cdot \text{sinc}(fT)$$

---

Sinc Function

Definition

The normalized sinc function is defined as:

$$\text{sinc}(t)=\frac{\sin (\pi t)}{\pi t}$$

with $\text{sinc}(0)=1$ (by L'Hôpital's rule or continuity).

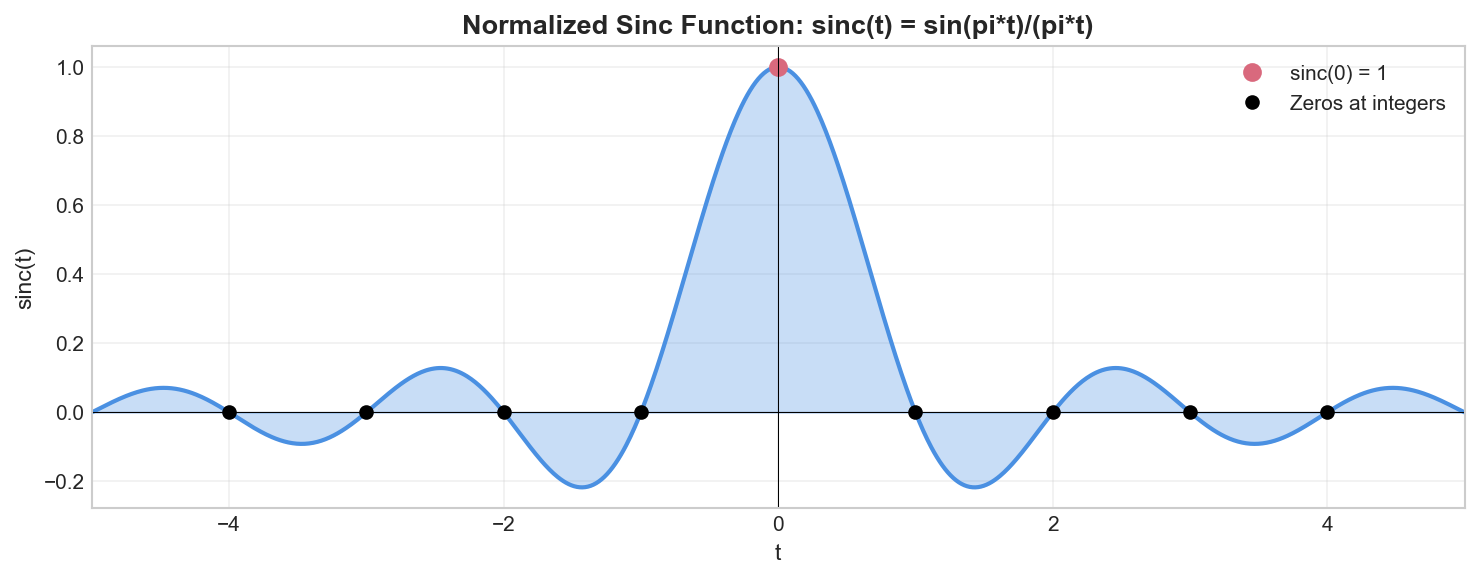
Properties

Zeros: $\text{sinc}(n)=0$ for all non-zero integers $n\in \mathbb{Z}\setminus \{0\}$

Normalization:

$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\text{sinc}(t)dt=1$$

Fourier Transform Pair: The sinc and rect functions are Fourier transform pairs:

$$\mathcal{F}\{\text{sinc}(t)\}=\text{rect}(f)$$$$\mathcal{F}\{\text{rect}(t)\}=\text{sinc}(f)$$

Ideal Lowpass Filter: The sinc function is the impulse response of an ideal lowpass filter.

Interpolation: The sinc function appears in the ideal reconstruction formula (Whittaker-Shannon interpolation).

---

Gaussian Pulse

Definition

The Gaussian pulse is defined as:

$$x(t)=e^{-\pi t^2}$$

More generally, with parameter $\alpha$:

$$x(t)=e^{-\alpha t^2}$$

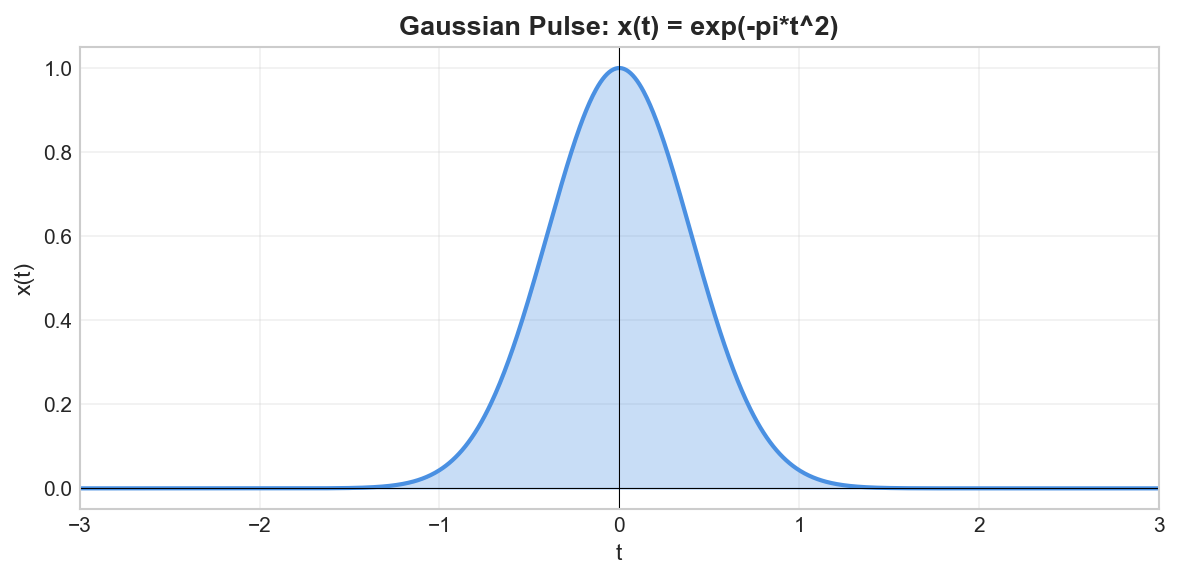
Properties

Self-Fourier Transform: The Gaussian is its own Fourier transform (with appropriate normalization):

$$\mathcal{F}\{e^{-\pi t^2}\}=e^{-\pi f^2}$$

Uncertainty Principle: The Gaussian achieves the lower bound of the time-frequency uncertainty principle:

$$\mathrm{\Delta }t\cdot \mathrm{\Delta }f\ge \frac{1}{4\pi }$$

Energy:

$$E={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{e}^{-2\pi t^2}dt=\frac{1}{\sqrt{2}}$$

Smoothness: The Gaussian is infinitely differentiable and has no discontinuities.

Summary

Signal	Definition	Key Property
Dirac delta $\delta (t)$	Unit impulse at $t=0$	Sifting property
Unit step $u(t)$	1 for $t\ge 0$, else 0	$\frac{du}{dt}=\delta (t)$
Unit ramp $r(t)$	$t$ for $t\ge 0$, else 0	$\frac{dr}{dt}=u(t)$
Complex exponential $e^{st}$	$e^{(\sigma +j{\omega }_0)t}$	Eigenfunction of LTI systems
Sinusoid	$A\cos ({\omega }_{0}t+\varphi )$	Periodic, period $T_0=2\pi /{\omega }_0$
Rectangular pulse	1 for $|t|\le T/2$	FT is sinc
Sinc	$\sin (\pi t)/(\pi t)$	FT is rect
Gaussian	$e^{-\pi t^2}$	Self-Fourier transform